Sigmoid激活函数

先介绍Sigmoid函数

$$ \sigma(x) = \frac{1}{1+e^{-x}} $$

这是二分类常用的一个拟合函数，它存在一些特性，例如：$\sigma(z) = 1-\sigma(-z)$

，$\sigma^{'}(z) = \sigma(z) (1-\sigma(z))$。在二分类中，当$y \in {0, 1}$，$\sigma(z)$表示取值概率。例如，如果我们定义损失函数如下：

$$ \mathbb{L} = -\left[ ylog\hat{y} + (1-y)log(1-\hat{y}) \right] $$

【导数】

$$ \begin{equation*} \begin{split} \frac{\partial} {\partial{x}} \sigma(x) &= \frac{\partial}{\partial{x}}\left( \frac{1}{1+e^{-x}} \right) \ &=\frac{(1)^’(1+e^{-x})-1(1+e^{-x})^’}{(1+e^{-x})^2} \ &= \frac{e^{-x}}{(1+e^{-x})^2} = \frac{(1+e^{-x})-1}{(1+e^{-x})^2} \ &= \frac{1}{(1+e^{-x})} - \frac{1}{(1+e^{-x})^2} \ &= \sigma(x) - \sigma(x)^2 = \sigma(x)(1-\sigma(x)) \end{split} \end{equation*} $$

Softmax

先看一张图看softmax函数的主要意图是什么：就是将一个多数值的的分布改写成概率分布：

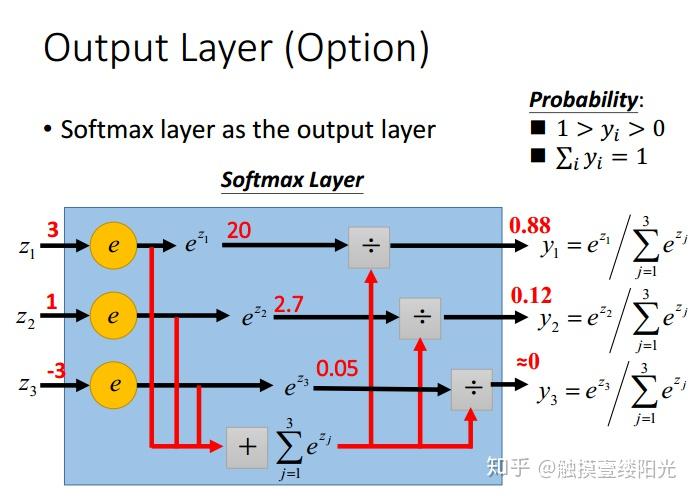
下面先回顾一下Softmax的函数定义：

$$ Softmax(z_i) = \sigma(z_i) = \frac{e^{z_i}}{\sum_{c=1}^C e^{z_c}} $$

从上图可以看到影响$y_1$的有与之关联的$z_1,z_2,z_3$。因此需要分别求出$\frac{\partial{y_1}}{\partial{z_1}},\ \frac{\partial{y_1}}{\partial{z_2}},\ \frac{\partial{y_1}}{\partial{z_3}}$。此时$y_1$的输出值为$y_1 = \frac{e^{z_1}}{e^{z_1}+e^{z_2}+e^{z_3}}$，很显然 $\frac{\partial{y_1}}{\partial{z_1}}$与$\frac{\partial{y_1}}{\partial{z_2}},\ \frac{\partial{y_1}}{\partial{z_3}}$的结果不同，而且后面部分的结果仅仅是索引号不同，求导结果的形式相同。因此在对Softmax函数求导的时候，需要分两种情况考虑。即对第$i$个输出节点，分为对$j=i$的$z_j$求导以及其它$j \neq i$的$z_j$求导。

对于 $j=i$时，Softmax的偏导数$\frac{\partial{y_i}}{\partial{z_j}}$可以展开为：

$$ \frac{\partial}{\partial{z_j}} \left( \frac{e^{z_i}}{\sum_{c=1}^C e^{z_c}} \right) = \frac{(e^{z_i})'(\sum_{c=1}^C e^{z_c}) - e^{z_i} (\sum_{c=1}^C e^{z_c})'} {(\sum_{c=1}^C e^{z_c})^2} \ = \frac{e^{z_i}(\sum_{c=1}^C e^{z_c}) - e^{z_i} e^{z_j}}{(\sum_{c=1}^C e^{z_c})^2} = \frac{e^{z_i}}{\sum_{c=1}^C e^{z_c}} \times \frac{\sum_{c=1}^C e^{z_c} - e^{z_j}}{\sum_{c=1}^C e^{z_c}} \ = \sigma(z_i) \times (1-\sigma(z_j)) $$

为了方便，我们可以将$\sigma(z_i)$表示为概率值$p_i$，那么求导结果为：$p_i(1-p_i)$

对于$j \neq i$时，类似前面介绍的$\frac{\partial{y_1}}{\partial{z_2}}$或$\frac{\partial{y_1}}{\partial{z_3}}$，Softmax的偏导数$\frac{\partial{y_i}}{\partial{z_j}}$可以展为

所以，综上可得，Softmax的导数求导为：

$$ \begin{equation*}

\frac{\partial{y_i}}{\partial{z_j}} = \left{ \begin{aligned} &\ p_i (1-p_j) , \ \ \ j = i, \ &-p_j \cdot p_j , \ \ \ j \neq i. \end{aligned} \right. \end{equation*} $$

定义$\delta_{ij}$，如果$i=j, \delta_{ij}=1, \text{ else } 0$：

$$ \frac{\partial y_i}{\partial z_j} = p_i \delta_{ij} - p_i p_j $$

可以看到推导还是比较复杂，但是推导结果很简单。

现在我们可以看一下对于Softmax激活函数常见的损失函数定义：交叉熵损失函数

我们先看Softmax的损失函数，回顾Softmax函数定义：$p_i = Softmax(z_i) = \frac{e_{e_i}}{\sum_{c=1}^C e^{z_c}}$

，其中$i$表示输出节点的编号。假设此时第$i$个节点为正确类目输出的节点，则$p_i$是正确类别对应的输出节点的概率值，我们可以添加$log$运算不影响函数单调性：$log(p_i) = log(\frac{e_{e_i}}{\sum_{c=1}^C e^{z_c}})$，我们目标是期望$p_i$越大越好，也就等价于最小化以下损失函数：$loss_i = - log(p_i) = -(z_i - log \sum_{c=1}^C e^{z_c})$，这就是Softmax的损失函数。大家看到这个公式可能会感到疑惑，因为我们通常使用的Softmax对应的损失函数是交叉熵损失函数，它的定义如下（大家应该也很熟悉）：

$$ \mathbb{L} = - \sum_{c=1}^C y_c \cdot log(\hat{y_c}) = - \sum_{c=1}^C y_c \cdot log(p_c) $$

公式中，$y_c$是真实标签值，$\hat{y_c}$是预测值，也就是计算出的softmax概率值$p_c$。

交叉熵损失函数和上面通过Softmax函数一步一步转换推导成的损失函数有什么区别？

为了方便描述我们将loss_i命名为公式一，$\mathbb{L}$命名为公式二。从下面的简单推导我们可以看出，其实公式一和公式二是等价的。

先给定一些假设：

对于分类任务来说，真实的样本标签通常表示为one-hot的形式。比如对于【三分类】来说，真实类别的索引位置为1，也就是属于第二个类别，那么使用one-hot编码表示为[0, 1, 0]，也就是仅正确类别位置为1，其余位置都为0。就是真实样本的标签值，将[0, 1, 0]分别代入公式一和公式二

公式一：

$$ loss_2 = -log(p_2) $$

公式二：

$$ \mathbb{L} = - \sum_{c=1}^C y_c \cdot log(\hat{y_c}) \ = -0 \cdot log(p_1) - 1\cdot log(p_2) - 0 \cdot log(p_3) \ = -log(p_2) = loss_2 $$

【交叉熵损失函数求导】

$$ \begin{equation*} \begin{split} \frac{\partial{\mathbb{L}}}{\partial{z_i}} &=

\sum_{c=1}^C y_c \cdot \frac{\partial{log(p_c)}}{\partial{p_c}} \cdot \frac{\partial{p_c}}{\partial{z_i}} \ &= - \sum_{c=1}^C y_c \cdot \frac{1}{p_c} \cdot \frac{\partial{p_c}}{\partial{z_i}} \ &= -y_i(1-p_i) + \sum_{c \neq i} y_c \cdot p_i \ &= -y_i + p_i (y_i + \sum_{c \neq i} y_c) \ &= p_i - y_i, \ 对于one-hot编码的多分类问题, \sum_c y_c = 1 \end{split} \end{equation*} $$

常见损失函数介绍

Sigmoid激活函数

Softmax

LambdaRank | XENDCG