前言
时间序列是指将同一统一指标的数值按其发生的时间先后顺序排列而成的数列。正如人们常说,人生的出场顺序很重要,时间序列中隐藏着一些过去与未来的关系。时间序列分析试图通过研究过去来预测未来。
时间序列分析在工程、金融、科技等众多领域有着广泛的应用。在大数据时代,时间序列分析已经成为AI技术的一个分支,通过将时间序列分析与分类模型相结合,更好的应用于数据检测、预测等场景。
时间序列与平稳性
在数学上,随机过程被定义为一族时间随机变量,即 ${x(t), t \in T}$,其中$T$表示$t$的变动范围。当$T={0, \pm1,\pm2,\dots}$时,此类随机过程$x(t)$是离散时间$t$的随机函数,称为时间序列。时间序列的构成要素有:
-
长期趋势$(T)$ :是在较长时间内受某种根本性因素作用而形成的总的变动趋势,具体表现通常是时间序列在某一方向上持续运动
-
季节变动$(S)$ :是在一年内随季节的变化而发生的有规律的周期性变动。它是诸如气候条件、生产条件、节假日或人们的风俗习惯等各种因素影响的结果。通常通过肉眼直接从序列图中比较难观察到这一现象,一般需要通过STL时间序列分解的方法来展示序列中的季节变动。
-
循环变动$(C)$ :是时间序列呈现出的非固定长度的周期性变动。循环波动的周期可能会持续一段时间,但与趋势不同,它不是朝着单一方向的持续变动,而是涨落相同的交替波动。(就是后面的序列相关性概念定义)
-
不规则变动$(I)$ :是时间序列中除去趋势、季节变动和周期波动之后的随机波动。不规则波动通常总是夹杂在时间序列中,致使时间序列产生一种波浪形或震荡式的变动。只含有随机波动的序列也称为平稳序列。(后面的随机噪声的定义)
-
序列相关性:时间序列的一个最重要特征是序列相关性,又称为相关性。从后面的图中可以看到,数据之间存在一定的正相关与负相关。例如某天的数据上升,它的前一天或者后一天也上升或者下降。自相关性是时间序列可以预测未来的前提(序列中存在的规律),如果没有自相关性,就变成了白噪声(无规律)。
-
随机噪声:它是时间序列除去趋势、季节变化和自相关性之后剩余的随机扰动。由于时间序列存在不确定性,随机噪声总是夹杂在时间序列中,致使时间序列表现出某种震荡式的无规律运动。
除非你的时间序列是平稳的,否则不能建立一个时间序列模型。在百度词条中是这样粗略描述的:平稳时间序列粗略地讲,一个时间序列,如果均值没有系统的变化(无趋势)、方差没有系统变化,且严格消除了周期性变化,就称之是平稳的。
平稳性的判断标准
判断一个序列是不是平稳序列的三个判断标准:
均值
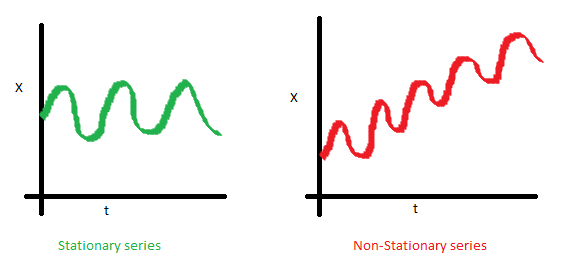
均值,是与时间$t$无关的常数。下图左边满足平稳序列条件,右边很明显具有时间依赖。
方差
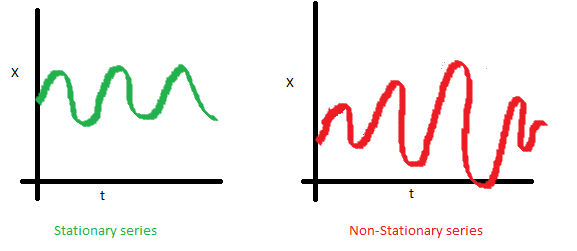
方差,是与时间$t$无关的常数。这个特性叫做方差齐性。下图显示了什么是方差对齐,什么不是方差对齐(注意右边图中的不同分布)
协方差
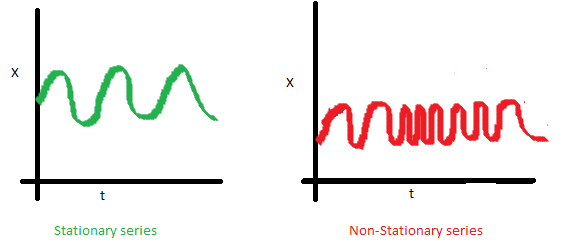
协方差,只与时间间隔$k$有关,与时间$t$无关的常数。如下图右图,可以注意到随着时间的增加,曲线变得越来越近。因此红色序列的协方差并不是恒定的
平稳性分类
时间序列的平稳性,和其它随机过程一样,分为严格平稳和宽平稳。
严平稳
如果对所有的时刻$t$,任意正整数$k$和任意$k$个正整数$(t_1,t_2,\cdots,t_k)$,$(r_{t1},r_{t2},\cdots,r_{tk})$的联合分布与$(r_{t1+t},r_{t2+t},\cdots,r_{tk+t})$的联合分布相同,我们称时间序列$r_t$是严平稳的。也就是,$(r_{t1+t},r_{t2+t},\cdots,r_{tk})$的联合分布在时间的平移变换下保持不变,这是个很强的条件。
宽平稳
若时间序列${r_t}$ 满足下面两个条件:$E(r_t)=\mu$,$\mu$是常数$Cov(r_t,r_{t-l})=r_l$,$r_l$只依赖于$l$,则时间序列${r_t}$为弱平稳的。即该序列的均值,$r_t$与$r_{t-l}$的协方差不随时间而改变,$l$为任意整数。
平稳性检测方法
在数学中,平稳随机过程(Stationary random process)或者严平稳随机过程(Strickly-sense stationary random process),又称为狭义平稳过程,是在固定时间和位置的概率分布与所有时间和位置的概率分布相同的随机过程:即随机过程的统计特性不随着时间的推移而变化。这样,数学期望和方差这些参数也不随时间和位置变化。平稳在理论上有严平稳和宽平稳两种,在实际应用上宽平稳使用较多。宽平稳的数学定义为:对于时间序列$y_t$,若对任意的$t,k,m$,满足:
$$ E(y_t) = E(y_{t+m}) cov(y_t,y_{t+k}) = cov(y_{t+k},y_{t+k+m}) $$
则称时间序列$y_t$是宽平稳的。
单位根校验
单位根校验是指检验序列中是否存在单位根,因为存在单位根就是非平稳时间序列了。Dickey-Fuller test和Augmented Dickey Fulley test(ADF)可以测试一个自回归模型存在单位根(unit root)。
为了保持单位和平均数相似,这里采用了标准差来代替方差:
|
|