语音识别是一个具有悠久历史的研究领域，从之前传统的统计模型，到目前热度很高的E2E框架，不断在刷新评测指标。这篇文章仅记录这个领域的一些里程碑时间和算法。如果想深入了解ASR整个领域的发展，可以从下面三个开源框架入手，后面有时间会补上ASR整个领域的综述性质的调研

Kaldi

WeNet

ESPnet

目前ASR存在三种比较成熟的E2E方案：CTC、RNN-T、Attention，主要有两个分支：① attention类，LAS为代表的，效果比较好，但是不能满足流式；② tansducers类，这类方案天然支持流式处理。

模型层从原来的transformer到现在conformer成为标准方案，目前各大模型的基线变成了conformer-t'ransduer。

另外，基于传统的语音识别技术依然是业界的主流方案，特别是在定制语言模型、处理OOV、快速修复bug等方面具有巨大的优势，而这恰恰是端到端语音识别方案薄弱的环节。

CTC

CTC最开始是Graves在ICML06会议上发表的一篇论文：Connectionist Temporal Classification: Labelling Unsegmented Sequence Data with Recurrent Neural Networks

，后来在他的博士论文中重新组织了公式，建立参考Graves的博士论文，因为Tensorflow中的代码实现参考的就是后面那篇博士论文（源码是“tensorflow/core/util/ctc/ctc_loss_calculator.h”），下面的介绍也是参考Graves的博士论文。

关于CTC的介绍也大量参考率网上其它的文章：

1. 一文读懂CRNN+CTC文字识别

2. CTC ALGORITHM EXPLAINED

3. Sequence ModelingWith CTC

4. CTC loss 笔记+源码分享(pytorch)

5. CTC 原理及实现

传统方案存在的问题

针对输入$x=(x_1,x_2,\dots,x_T)$，输出label seqence $y=(y_1,y_2,\dots,y_L)$，传统的方案是假设$x_i$和$y_j$之间是对齐的，即$x_i \rightarrow y_i, T=L$。但是在一些应用场景，$x_i$和$y_j$之间很难建立起这种映射关系，或者说代价很大。例如，在语音识别场景、OCR场景。CTC算法提出来就是为了解决这类问题。

下面的两个图的对比能比较直观的给出上述区别：

图一：传统rnn只能一对一输出（当然seq2seq框架能解决这个问题）

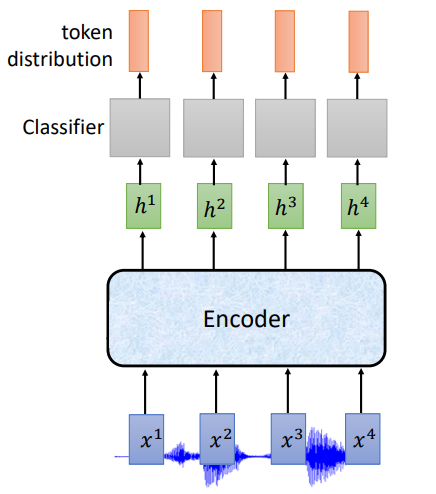
而CTC通过在输出词汇表中加入一个空的标记符来解决，这时词典大小编程$|V|+1$

图二：CTC的解决方案

从上图也可以看出，CTC方案存在缺陷，例如最后一个例子输出是好棒棒，显然不合理，后文会分析这个问题以及对应的解决方案。

公式推导

在正式开始公式推导前，为了后续描述方便，预先给出一些符号定义。

• $L$：标签集合空间，例如英文OCR任务，空间集合是26个英文字母（假设不包含标点符号等）。$\left|L\right|$ 标签空间大小

• $L'$：$L \cup {blank}$

• $\mathbf S$：训练集

• $\pi$：一条路径，描述了生成最终标签序列的一条路径，通常 $\pi \in L'^T$，具体表示了一条长度为$T$的路径（路径的具体含义可以参考下文中展开的具体描述）

• $p(\pi | \mathbb x, \mathbf S) = \prod {t=1} ^T y{\pi t}^t$：$y{\pi_t}^t$ is the activation of output unit $\pi_t$ at time $t$

• $\mathcal{B}: L'^T \rightarrow L^{\le T}$：表示从一条路径$\pi \in L'^T$到label seqence的映射。例如： $\mathcal{B}(\text{-a-pp-plle}) = \mathcal{B}(\text{a--p-p-ll-e-})= \text{apple}$，'-'表示blank字符。其中映射规则是将空格移除，重复字符合并

• $p(\mathbf l | x) = \sum_{\pi \in {\mathcal{B}^{-1}(\mathbf I)}} p(\pi | x)$，其中$\mathbf{l} \in L^{\le T}$，表示一个具体的labeling sequence

• $\alpha_t(s)$：在t时刻，路径$\pi$的标签为s的子路径$\pi_{1:t}$概率（具体定义见下文的Forward Probability）

• $\beta_t(s)$：在t时刻，路径\pi的标签为s的子路径$\pi_{t+1:|L'|}$概率（具体定义见下文的Backward Probability）

Label Transition Matrix

Label Transition Matrix这个名字是自己取的，感觉比较形象。

首先举一个例子，label seqence是 state，首先构建$L' = \text{-s-t-a-t-e}$，构建规则是：在label序列的每个token之间，以及收尾加上blank字符（这里blank字符使用'-'表示）

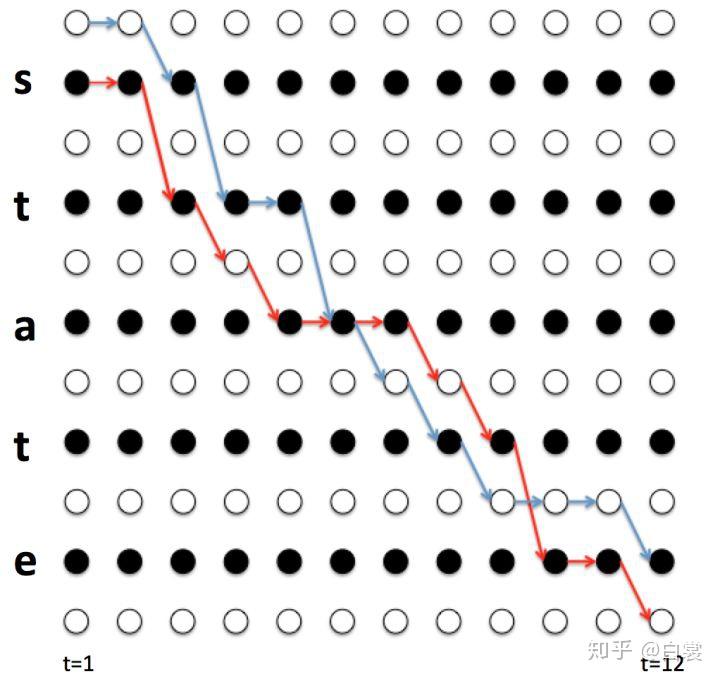
生成label sequence的过程如下：从矩阵图的左上角开始，只能往右 和 下两个方向移动，在右下角结束，每次移动一步，生成一个具体的label $s \in L$，或者一个blank label。左上角起始位置只能选择 blank或者s，右下角结束位置只能是 e或者 blank。上图给出了生成state的两条路径：$\pi_1 = \text{(--stta-tee-)},\ \pi_2=\text{sst-aaa-tee-}$，这两条路径都对应了相同的label sequence：state。这里的$\pi_1,\pi_2$就是上面提到的路径$\pi$的概念。从上图可以看到，一个具体的label seqence对应的路径数量可以枚举，但是数量太大，直接枚举计算不现实，Graves因此提出了CTC算法来解决这个问题，主要是通过动态规划算法来分而治之。其中关键的概念是Forward Probability和Backward Probability

1. Forward Probability

下面借用Graves Thesis的定义来阐述向前概率：

For a labeling l, we define the forward probability variables $\alpha_t(s)$ as the summed probability of all paths whose length t prefixes are mapped by $\mathcal{B}$ onto the length s/2 prefix of l, ie:

$\alpha_t(s) = P(\pi_{1:t}:\mathcal{B}(\pi_{1:t})=\mathbb{l}{1:s/2},\pi_t=l_s^{'}|x) = \sum\limits{\substack{\pi:\ \mathcal{B}(\pi_{1:t})=\mathbb{l}{1:s/2}}} \prod\limits{t'=1}^t y_{\pi_{t'}}^{t'}$

where, for some sequence $s$, $s_{a:b}$ is the subsequence $(s_a,s_{a+1}, \dots, s_{b-1},s_b)$, and $s/2$ is rounded down to an integer value.

简而言之，$\alpha_t(s)$是所有经过节点$s$的路径$\pi$，每条路径从开始节点到$s$节点的子节点的概率之和。给定了上面的向前概率定义，我们可以使用动态规划算法来计算：

$p(l|x) = \alpha_T(|l'|) + \alpha_T(|l'|-1)$

上面等式右边的第一项是路径$\pi$以blank结尾的概率，第二项是以序列最后一个label结尾的概率。结合state这个标签序列为例子，在t=12的时候，结尾的label只能是blank或者e这两个标签（大家可以回忆前面基于标签序列$L$构建$L'$的介绍，$|L'|=2|L|+1$）,从上面的公式可以看出我们可以递归求解上述问题：

$$ \begin{equation} \begin{split} \alpha_1(1) = y_b^1 \ \alpha_1(2) = y_{l_1}^1 \ \alpha_1(s) = 0, \forall s>2 \end{split} \end{equation} $$

$$ \begin{equation} \alpha_t(s) = y_{l's}^t \times \left{ \begin{aligned} & \alpha{t-1}(s)+\alpha_{t-1}(s-1), \text{ if } l's=b \text{ or } l'{s-2}=l's \text{ ①} \ & \alpha{t-1}(s)+\alpha_{t-1}(s-1)+\alpha_{t-1}(s-2), \text{ otherwise, ②} \ & 0,\text{ } \forall s < |l'|-2|T-t|-1， \text{ ③} \end{aligned} \right.

\end{equation} $$

对于公式(2)里三种情况：

1. 这种情况参考下图。如果当前时刻t的标签$s=\epsilon \text{, or } l's = l'{s-2}$，那么在t-1时刻s可能的取值为$s \in {s, s-1}$ （这里需要仔细琢磨一下，需要确保加入t时间的标签后多条路径的概率计算保持相等）

   

2. 参考下图，当前时刻t的标签为非空标签，那么前一个标签必然为空，前两个标签为有效并且与当前标签不等的标签，因此有三条路径

   

3. 其它路径都是非法的，因为剩余标签没有足够的time steps来输入

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61

// tensorflow示例代码(tensorflow/core/util/ctc/ctc_loss_calculator.h)
template <typename TT>
void CTCLossCalculator<TT>::CalculateForwardVariables(
    const std::vector<int>& l_prime, const Matrix& y, bool ctc_merge_repeated,
    Matrix* log_alpha) const {
  using Eigen::numext::log;

  // Number of cols is the number of time steps = number of cols in target
  // after the output delay.
  // U: 转移矩阵的序列长度，即加入空白字符的标签序列长度
  // T: 输入x的长度
  // log_alpha shape: (U, T)
  log_alpha->setConstant(kLogZero<TT>());

  int U = l_prime.size();
  int T = log_alpha->cols();

  CHECK_EQ(U, log_alpha->rows());

  // Initial alpha values in (GravesTh) Eq 7.5 and Eq 7.6.
  // 参看上面的公式 (1)，初始化，注意这里的t和s起始索引从 0 开始，公式里从 1 开始
  // (0, 0) 第一个 0 表示 s 值，第二个 0 表示 t 
  log_alpha->coeffRef(0, 0) = log(y(blank_index_, output_delay_));
  // Below, l_prime[1] == labels[0]
  auto label_0 = (l_prime.size() > 1) ? l_prime[1] : blank_index_;
  log_alpha->coeffRef(1, 0) = log(y(label_0, output_delay_));

  for (int t = 1; t < T; ++t) {
    // If there is not enough time to output the remaining labels or
    // some labels have been skipped, then let log_alpha(u, t) continue to
    // be kLogZero.
    for (int u = std::max(0, U - (2 * (T - t))); u < std::min(U, 2 * (t + 1));
         ++u) {
      // Begin (GravesTh) Eq 7.9
      // Add in the u, t - 1 term.
      auto sum_log_alpha = kLogZero<TT>();
      if (ctc_merge_repeated || l_prime[u] == blank_index_) {
        sum_log_alpha = log_alpha->coeff(u, t - 1);
      }

      // Add in the u - 1, t - 1 term.
      if (u > 0) {
        sum_log_alpha =
            LogSumExp(sum_log_alpha, log_alpha->coeff(u - 1, t - 1));
      }

      // Add in the u - 2, t - 1 term if l_prime(u) != blank or l_prime(u-2).
      if (u > 1) {
        const bool matching_labels_merge =
            ctc_merge_repeated && (l_prime[u] == l_prime[u - 2]);
        if (l_prime[u] != blank_index_ && !matching_labels_merge) {
          sum_log_alpha =
              LogSumExp(sum_log_alpha, log_alpha->coeff(u - 2, t - 1));
        }
      }
      // Multiply the summed alphas with the activation log probability.
      log_alpha->coeffRef(u, t) =
          log(y(l_prime[u], output_delay_ + t)) + sum_log_alpha;
    }  // End (GravesTh) Eq 7.9.
  }
}

2. Backward Probability

后向概率计算与前向概率计算类似，不展开描述，直接给出公式（参考Graves的博士论文），下面先给出后向概率的定义：

The backword probability variables $\beta_t(s)$ are defined as the summed probability of all paths whose suffixes starting at $t+1$ map onto the suffix of l starting at label $s/2$. $\beta_t(s) = P(\pi_{t+1:T}:\mathcal{B}(\pi_{t+1:T})=\mathbb{l}{s/2:|\mathbb{l}|},\pi_t=l_s^{'}|x) = \sum\limits{\substack{\pi:\ \mathcal{B}(\pi_{t+:T})=|\mathbb{l}|{s/2:\mathbb{l}}}} \prod\limits{t'=t+1}^T y_{\pi_{t'}}^{t'}$

$$ \begin{equation} \begin{split} \beta_T(|\mathbb{l}'|) = 1\ \beta_T(|\mathbb{l}'-1|) = 1\ \beta_T(s) = 0, \forall s < |\mathbb{l}'|-1 \end{split} \end{equation} $$

$$ \begin{equation} \beta_t(s) = y_{l's}^t \times \left{ \begin{aligned} & \beta{t+1}(s)+\alpha_{t+1}(s+1), \text{ if } l's=b \text{ or } l'{s+2}=l's \text{ ①} \ & \beta{t+1}(s)+\alpha_{t+1}(s+1)+\alpha_{t+1}(s+2), \text{ otherwise, ②} \ & 0,\text{ } \forall s > 2t \text{ or } s>|\mathbb{l'}|， \text{ ③} \end{aligned} \right.

\end{equation} $$

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

template <class TT>
void CTCLossCalculator<TT>::CalculateBackwardVariables(
    const std::vector<int>& l_prime, const Matrix& y, bool ctc_merge_repeated,
    Matrix* log_beta) const {
  // Number of cols is the number of time steps =  number of cols in target.
  // Matrix log_beta =
  //    Matrix::Constant(l_prime.size(), y.cols() - output_delay_,
  // kLogZero);
  using Eigen::numext::log;

  log_beta->setConstant(kLogZero<TT>());
  int T = log_beta->cols();
  int U = l_prime.size();
  CHECK_EQ(U, log_beta->rows());

  // Initial beta values in (GravesTh) Eq 7.13: log of probability 1.
  for (int u = U - 2; u < U; ++u) log_beta->coeffRef(u, T - 1) = 0;

  for (int t = T - 1 - 1; t >= 0; --t) {
    // If there is not enough time to output the remaining labels or
    // some labels have been skipped, then let log_beta(u, t) continue to
    // be kLogZero.
    for (int u = std::max(0, U - (2 * (T - t))); u < std::min(U, 2 * (t + 1));
         ++u) {
      // Begin (GravesTh) Eq 7.15
      // Add in the u, t + 1 term.
      if (ctc_merge_repeated || l_prime[u] == blank_index_) {
        log_beta->coeffRef(u, t) =
            LogSumExp(log_beta->coeff(u, t),
                      log_beta->coeff(u, t + 1) +
                          log(y(l_prime[u], output_delay_ + t + 1)));
      }

      // Add in the u + 1, t + 1 term.
      if (u + 1 < U) {
        log_beta->coeffRef(u, t) =
            LogSumExp(log_beta->coeff(u, t),
                      log_beta->coeff(u + 1, t + 1) +
                          log(y(l_prime[u + 1], output_delay_ + t + 1)));
      }

      // Add in the u + 2, t + 1 term if l_prime(u) != blank or l_prime(u+2).
      if (u + 2 < U) {
        const bool matching_labels_merge =
            ctc_merge_repeated && (l_prime[u] == l_prime[u + 2]);
        if (l_prime[u] != blank_index_ && !matching_labels_merge) {
          // Add in u + 2 term.
          log_beta->coeffRef(u, t) =
              LogSumExp(log_beta->coeff(u, t),
                        log_beta->coeff(u + 2, t + 1) +
                            log(y(l_prime[u + 2], output_delay_ + t + 1)));
        }
      }  // End (GravesTh) Eq. 7.15
    }
  }
}

Loss计算

优化目标是最大化标签序列的概率似然函数，损失函数则是简单的概率似然函数的负数：

$$ \begin{equation} \mathcal{O} = -ln\left( \prod\limits_{(x,z) \in \mathcal{S}} p(z|x) \right) = -\sum\limits_{(x,z) \in \mathcal{S}} ln p(z|x) \end{equation} $$

要求出公式(5)的偏导数，首先要计算标签$z$的概率 $p(z|x)$ （这里的符号$z$表示的是实际输出的标签序列）

首先，我们可以根据$\alpha_t(s)\text{和}\beta_t(s)\text{的定义得到}\alpha_t(s)\beta_t(s)$：

$$ \begin{equation} \alpha_t(s) \beta_t(s) = \sum\limits_{\substack{\pi \in \mathcal{B}^{-1}(z)\ \pi_t=z's}} \prod\limits{t=1}^T y_{\pi_t}^t = \sum\limits_{\substack{\pi \in \mathcal{B}^{-1}(z)\ \pi_t=z'_s}} p(\pi|x) \end{equation} $$

公式(6)其实就是一条经过标签节点s的概率，使用$z'$代表路径$pi$，$z$表示目标标签序列：

$$ \begin{equation} p(z|x) = \sum\limits_{s=1}^{|z'|} \alpha_t(s) \beta_t(s) \end{equation} $$

上面公式中的t实际上是一个常量，在TensorFlow的源码中选取$t=0$来计算：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

template <class T>
template <typename VectorIn, typename VectorOut, typename MatrixIn,
          typename MatrixOut>
Status CTCLossCalculator<T>::CalculateLoss(
    const VectorIn& seq_len, const LabelSequences& labels,
    const std::vector<MatrixIn>& inputs, bool preprocess_collapse_repeated,
    bool ctc_merge_repeated, bool ignore_longer_outputs_than_inputs,
    VectorOut* loss, std::vector<MatrixOut>* gradients,
    DeviceBase::CpuWorkerThreads* workers) const {

     ......
 // The loss is computed as the log(p(z|x)) between the target and
      // prediction. Do lazy evaluation of log_prob here.
      T log_p_z_x = kLogZero<T>();
      for (int u = 0; u < l_prime.size(); ++u) {
        // (GravesTh) Eq 7.26, sum over all paths for t = 0.
        log_p_z_x = LogSumExp(log_p_z_x, log_alpha_b(u, 0) + log_beta_b(u, 0));
      }

      (*loss)(b) = -log_p_z_x;  // Use negative log loss for display.
    ......
}

Gradient

梯度计算可以应用链式法则来计算，先回顾和定义我们将使用到的一些符号：

$$ \begin{aligned} & y_k^t: \text{在t时刻标签为k的概率，这个数值一般是softmax网络层的输出, } (y_0^t, y_1^t, \dots, y_k^t, \dots, y_C^t)\ & lab(z,k) = {s : z'_s = k} \text{：出现在z'序列中标签为k的s下标集合} \end{aligned} $$

$$ \begin{equation} \frac{\partial \alpha_t(s) \beta_t(s)}{\partial y_k^t} = \left{ \begin{aligned} &\frac{\alpha_t(s) \beta_t(s)} {y_k^t} \text{, if k occurts in z'} \
&0 \text{, otherwise} \end{aligned} \right.

\end{equation} $$

结合公式(7)和公式(8)，得到$p(z|x)$的导数如下：

$$ \begin{equation} \frac{\partial p(z|x)}{\partial y_k^t} = \frac{1}{y_k^t} \sum\limits_{s \in lab(z,k)} \alpha_t(s) \beta_t(s) \end{equation} $$

结合公式(5)和(8)：

$$ \frac{\partial O} {\partial y_k^t} = - \frac{1}{p(z|x) y_k^t} \sum\limits_{s \in lab(z,k)} \alpha_t(s) \beta_t(s) $$

输入到CTC的输入层是经过softmax后的概率分布，假设在最后一层的输入是$u_k^t=(u_0^t,u_1^t, \dots, u_C^t)$，我们需要计算$\frac{\partial y_{k'}^t}{\partial u_k^t}$:

$$ \frac{\partial y_{k'}^t}{\partial u_k^t} = y_{k'}^t \delta_{kk'} - y_{k'}^t y_k^t,\ \delta_{kk'}=1 \text{ if }k=k' , \text{ else } \delta_{kk'}=0 $$

最终的梯度公式如下：

$$ \begin{equation} \begin{aligned} \frac{\partial O} {\partial u_k^t} &= - \sum\limits_{k'} \frac{\partial O}{\partial y_{k'}^t} \frac{\partial y_{k'}^t}{\partial u_k^t} \ &= y_k^t - \frac{1}{p(z|x)} \sum\limits_{s \in lab(z,k)} \alpha_t(s) \beta_t(s) \text{， ?最后一步没推导出来！}

\end{aligned} \end{equation} $$

梯度的公式推导最后部分没大看懂，待后续研读之后再补充这部分

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

// Using (GravesTh) Eq 7.26 & 7.34.
template <typename TT>
void CTCLossCalculator<TT>::CalculateGradient(const std::vector<int>& l_prime,
                                              const Matrix& y,
                                              const Matrix& log_alpha,
                                              const Matrix& log_beta,
                                              TT log_p_z_x, Matrix* dy) const {
  // Only working with the leftmost part of dy for this batch element.
  auto dy_b = dy->leftCols(y.cols());

  // It is possible that no valid path is found if the activations for the
  // targets are zero.
  if (log_p_z_x == kLogZero<TT>()) {
    LOG(WARNING) << "No valid path found.";
    dy_b = y;
    return;
  }

  int L = y.rows();
  int T = y.cols();
  int U = l_prime.size();

  for (int t = 0; t < T - output_delay_; ++t) {
    Array prob_sum(L);
    prob_sum.setConstant(kLogZero<TT>());

    for (int u = 0; u < U; ++u) {
      int l = l_prime[u];
      prob_sum[l] = LogSumExp(prob_sum[l], log_alpha(u, t) + log_beta(u, t));
    }

    for (int l = 0; l < L; ++l) {
      // Negative term in (GravesTh) Eq 7.28.
      auto negative_term = expf(prob_sum[l] - log_p_z_x);

      dy_b(l, output_delay_ + t) = y(l, output_delay_ + t) - negative_term;
    }
  }
}

CTC方案的缺陷

这里引用知乎上的一个图片来介绍会让大家有更加直观的理解：

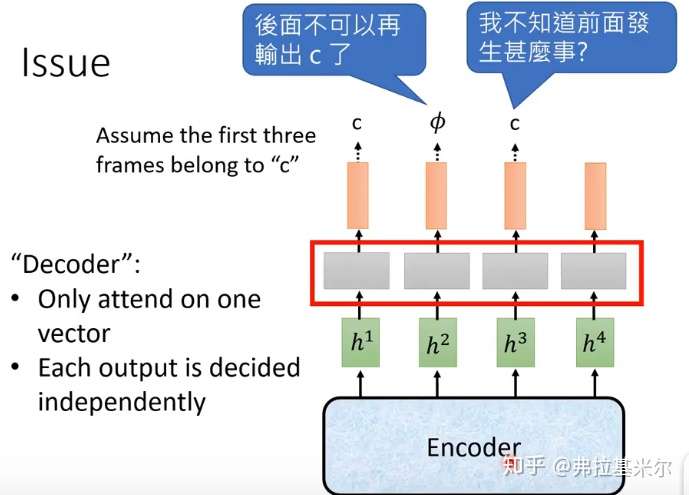
CTC存在的问题：

1. 每一次输出结果都是独立的

2. 可能会出现重复输出的问题

其中第二个问题的深层次原因还是由于问题一引起的。上图是一个例子，假设前面三帧输入对应的输出是三个连续的ccc，按照CTC的映射函数$\mathcal{B}$连续字符的输出是一个c，但是由于中间的识别问题输出了一个非空字符$\mathit {\Phi}$，导致输出为cc。

Rnn-T ( Rnn Transducer)

RNN-T 文章是Graves 2012年提出来的，主要是针对CTC的独立性假设缺陷的改进方案。

下面先给出文章里的一些符号定义：

$x=(x_1,x_2,\dots,x_T) \in \mathcal{X^*}$：输入序列

$y=(y_1,y_2,\dots,y_U) \in \mathcal{Y^*}$：输出序列

$\tilde {\mathcal{Y}} = \mathcal{Y} \cup \mathit{\Phi}$：扩展输出空间

$\alpha$：定义一个对齐的路径，通过映射函数$\mathcal{B}$可以映射到一个真实的$y$序列，例如$\alpha=(y_1,\mathit{\Phi},\mathit{\Phi},y_2,\mathit{\Phi},y_3)$经过$\mathcal{B}(\alpha)$映射等于$y=(y_1,y_2,y_3)$

$\mathcal{B}$：映射函数，实现$\tilde{\mathcal{Y}^} \rightarrow \mathcal{Y}^$的映射

模型整体目标函数：

$$ \begin{equation} P(y \in \mathcal{Y}^*|x) = \sum\limits_{\alpha \in \mathcal{B}^{-1}} P(\alpha|x) \end{equation} $$

整体模型框架如下图：

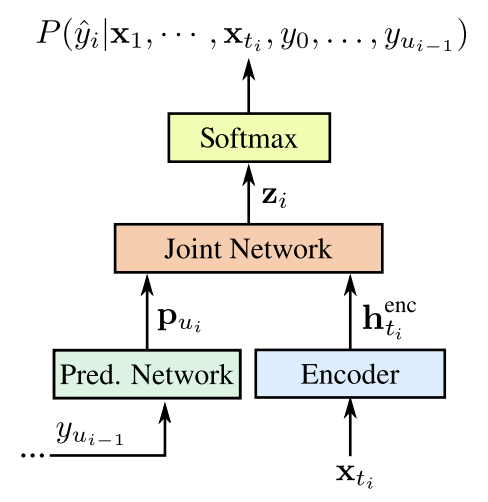
RNN-T模型引入了TranscriptionNet也就是图中的Encoder（可以使用任何声学模型的结构），相当于声学模型部分，图中的PredictionNet实际上相当于语言模型（可以使用单向的循环神经网络来构建）。模型中比较新奇，同时也是最重要的结构就是联合网络Joint Net，一般可以使用前向网络来进行建模。联合网络的作用就是将语言模型和声学模型的状态通过某种思路结合在一起，可以是拼接操作，也可以是直接相加等，考虑到语言模型和声学模型可能有不同的权重问题，似乎拼接操作更加合理一些。但是论文中使用的是加法操作。

Transcription Network $\mathcal{F}$

转录网络$\mathcal{F}$就是图中的Encoder，将输入$x$转换成向量$f=(f_1,f_2,\dots,f_T)$，

$$ \begin{equation} \begin{aligned} &\overleftarrow{h_t} = \mathcal{H}\left( W_{i\overleftarrow{h}} i_t + W_{\overleftarrow{h}\overleftarrow{h}} \overleftarrow{h}{t+1} + b{\overleftarrow{h}} \right)\

&\overrightarrow{h_t} = \mathcal{H}\left( W_{i\overrightarrow{h}} i_t + W_{\overrightarrow{h}\overrightarrow{h}} \overrightarrow{h}{t-1} + b{\overrightarrow{h}} \right)\ &o_t = W_{\overrightarrow{h}o} \overrightarrow{h}t + W{\overleftarrow{h}o} \overleftarrow{h}_t + b_o \end{aligned} \end{equation} $$

最终转录网络的输出为$f_t$，是一个$K+1$向量（$K$是输出标签空间大小）

Prediction Netowrk $\mathcal{G}$

预测网络$\mathcal{G}$将目标向量$\hat{y}=(\Phi,y_1,y_2,\dots,y_U)$转换成向量$g=(g_0,g_1,\dots,g_U)$，类似于语言模型作用（注意，这里的长度是$U+1$）,RNN网络使用的是LSTM

$$ \begin{equation} \begin{aligned} &h_u = \mathcal{H}(W_{ih} \hat{y_u} + W_{hh} h_{u-1} + b_h)\ &g_u = W_{ho} h_u + b_o \end{aligned} \end{equation} $$

针对序列输入中某一时刻t的输入 $y_t$，是一个$K$维的onehot向量，例如如果$y_t=k$，那么$k^{th}$位置为1，其余都为0。而$\mathit{\Phi}$是全为0的$K$维向量。输出层为$K+1$维向量（多出的一个维度是扩展的$\Phi$）。也就是说，输出的$g_u$也是$K+1$维向量。

Joint Network

联合网络将$\mathcal{G}$和$\mathcal{F}$合并之后输出一个概率密度函数（类似于softmax）。给定转录输出向量$f_t, 1\le t \le T$，预测网络输出向量$g_u, 0 \le u \le U$，标签$k \in \tilde{Y}$，概率密度函数为：

$$ \begin{equation} h(k,t,u) = exp(f_t^k + g_u^k) \end{equation} $$

其中$k$表示向量的第 $k^{th}$元素，归一化后的密度函数为：

$$ \begin{equation}

P(k \in \tilde{Y} | t,u) = \frac{h(k,t,u)}{\sum_{k' \in \tilde{Y}} h(k',t,u)} \end{equation} $$

可以看到RNN-T通过Prediction Network $\mathcal{G}$和JoinNet引入了Token之间的相关性，下面给一个图简单介绍一下它整体的优化目标计算逻辑，和CTC有些类似，也引入了forward & backward variable。

为了解析路径概率，RNN-T使用了一张概率转移图，如下所示：

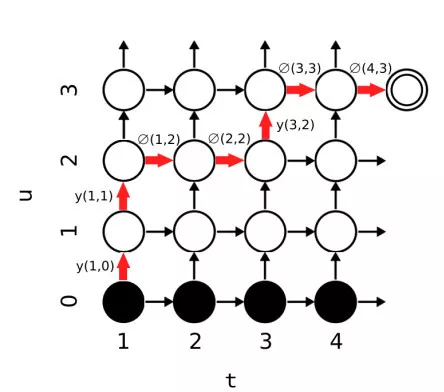
概率转移矩阵中的横坐标t表示声学输入编码后的状态$f_t$，纵坐标表示预测标签编码后的$g_u$。在介绍如何利用图示的概率转移矩阵计算路径概率前先引入以下公式定义：

$$ \begin{equation} \begin{aligned} \alpha(t,u) &= \alpha(t-1,u)\mathit{\Phi}(t-1,u) \ &+ \alpha(t,u-1)y(t,u-1) \ \beta(t,u) &= \beta(t+1,u)\mathit{\Phi}(t,u) \ &+ \beta(t,u+1)y(t,u) \ \alpha(0,1) &=1 \ \beta(T,U) &= \mathit{\Phi}(T,U) \ P(y|x) &= \alpha(T,U) \mathit{\Phi}(T,U) \end{aligned} \end{equation} $$

首先，$\alpha(t,u)$定义了向前变量，含义是读取前t个输入$f_{[1:t]}$输出是$y_{[1:u]}$的概率。同理，$\beta(t,u)$定义了向后变量，含义是读取从t+1开始到最后一个输入为止的编码后输入特征$f_{[t+1:T]}$，输出概率是$y_{[u+1:U]}$。

• 在概率转移矩阵中，(t,u)节点表示在输入前t个，输出前u个元素的概率。

• 横坐标方向移动（横移）表示输出空间点概率，即 $\mathit{\Phi}(t,u)$，意味着在$(t,u)$为止输出为空；纵坐标方向移动（纵向）表示输出纵坐标对应标签的概率，即 $y(t,u)$是输出$y的(u+1)^{th}$标签的概率。

• 完成解析路径从左下角开始，在右上角结束。底部黑色节点表示在空节点

从上图红线标注的解码过程我们很显然可以看到一个缺陷：声学模型根据第一个输入，输出了两个标签。例如假设目标标签序列是'hello'，在处理第一个声学输入之后，输出了两个标签h e，显然很多情况下这是不合理的，因此一种对模型增加一种合理的约束，使得模型没解码一个语言模型的状态均需要消耗掉一个声学模型状态，也就是时间步加一。上述问题的根源在于解析过程中计算了从起点到终点所有可能的路径，但是很多路径其实是不合理的，我们需要有一种约束来减少无效空间的搜索。

为了更好的理解RNN-T中的对齐操作，我们使用另外一个例子来讲解。

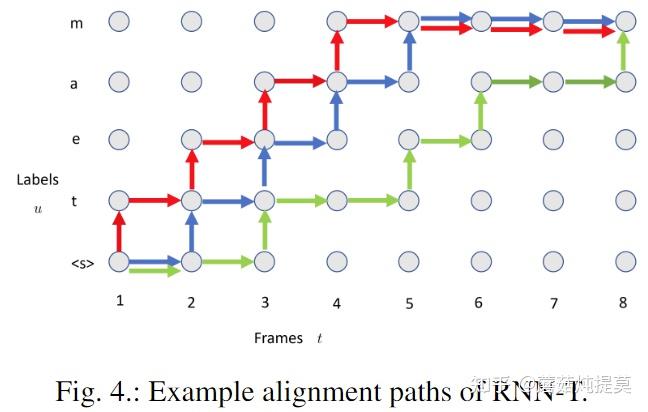
上图中为语音序列$x=(x_1,x_2,\dots,x_8)$ 和标签序列$y=\text{(, t, e, a, m)}$ 绘制了三个对齐路径示例，其中$$是句子开始的记号。所有有效的对其路径都是从$T\times U$网格左下角到右上角，因此每个对齐路径长度是$T+U$。在对齐路径中，水平箭头通过以空白标签保留预测网络状态并前进一个时间步长，而垂直箭头发出一个非空白输出标签。

虽然RNN-T现在是最自然的端到端流媒体模型，但普通RNN-T仍然面临延迟挑战，因为RNN-T倾向于延迟输出其预测结果，直到通过获得更多未来帧进而产生更高的confidence之后才输出。图4中的绿色路径就是这种延迟决策的示例。为了保证RNN-T的低延迟，有论文提出采用强制对齐的方式，将训练的结果同真实结果之间的对齐强制限制在某一个时间阈值内，并禁止其他对齐路径。输入语音序列和输出标签序列之间的严格对齐，以便为流式RNN-T生成更好的对齐方式。除了延迟的好处之外，所有这些强制对齐RNN-T方法的另一个优点是节省GPU内存和训练加速，因为它们在训练期间使用了较少的对齐路径。

下面将介绍谷歌的RNA模型(Recurrent Neural Aligner)。

Recurrent Neural Aligner

论文

模型框架如下图：

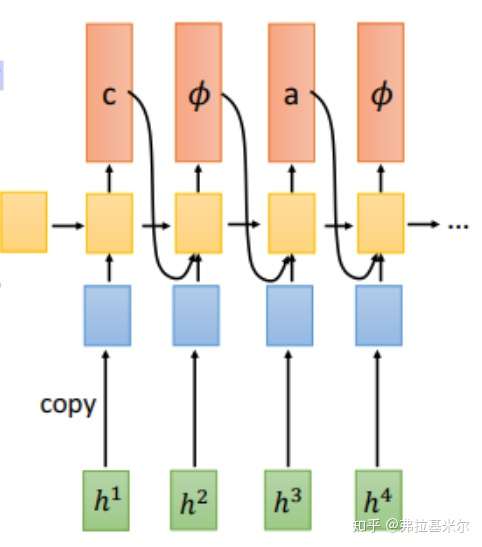
RNA模型使用RNN做为encoder，在decode的时候，有一个假设：输入序列长度大于等于输出序列长度。另外，每个输入对应一个输出（如下图所示），而RNN-T一个输入可能对应多个输出。通过这个限定，RNA的解码搜索空间要小于RNN-T。此外，解码使用了forward-backward algorithm，细节可以参考论文，这里不再展开介绍。

Neural Transducer

LAS

MoChA